

You can also enter the numbers with %, like "2% 10% -10% 8%" and will deal with that as well (it simply strips the %). Our geometric mean calculator handles this automatically, so there is no need to do the above transformations manually. The geometric mean is 1.0256 which equals 2.56% average growth per year. The total growth at the end is 7.89%, but how do we calculate the average yearly growth rate? 10% would usually be -10%, having a different sign and forbidding us from doing the calculation, but we can do a little trick and express the numbers as proportions, thus 8% growth becomes 1 + 8% x 1 = 1.08, 10% decline becomes 1 - 10% x 1 = 0.9 and 11% growth becomes 1 + 11% x 1 = 1.11. Let's say we have the following relative changes in 3 consecutive years: 8% growth, 10% decline, 11% growth. However, this doesn't mean we can't work with negative numbers as well. Geometric mean for negative numbersįrom the definition we can see that we can only calculate the geometric mean of positive numbers, or, more precisely, the numbers need to be of the same sign, in order to avoid taking the root of a negative product, which would result in imaginary numbers. However, before settling on using the geometric mean, you should consider if it is the right statistic to use to answer your particular question. For example, replacing 30 with 100 would yield an arithmetic mean of 25.80, but a geometric mean of just 9.17, which is very desirable in certain situations. This can be verified by our geometric average calculator as well.Īs you can see, the geometric mean is significantly more robust to outliers / extreme values. The arithmetic mean of the exponents (1 and 3) is 2, so the geometric mean is 2 2 = 4. It is handy to use log with base 2 here, so 2 = 2 1 and 8 = 2 3. Let's say you want to calculate the geomean of 2 and 8. This is equivalent to raising 19,500 to the 1/5-th power.Īnother way to calculate the geometric mean is with logarithms, as it is also the average of logarithmic values converted back to base 10. To calculate the geometric mean, we take their product instead: 1 x 5 x 10 x 13 x 30 = 19,500 and then calculate the 5-th root of 19,500 = 7.21. We would just sum the numbers (1 + 5 + 10 + 13 + 30) and then divide by 5, giving us an arithmetic mean of 11.80. Let's say we have a set of numbers: 1 5 10 13 30 and we want to calculate their arithmetic mean.
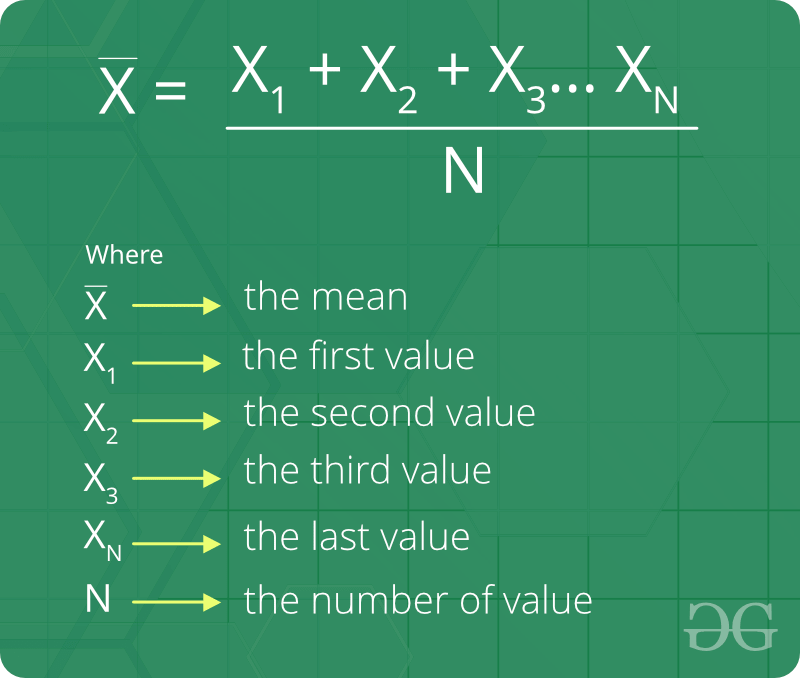
In the image above the perimeter calculation corresponds to the arithmetic mean and the area calculation - to the geometric mean.Īssuming you don't want to use a calculator, obviously. The geometric mean answers the question: what side should a square have so that its area is 64? The answer is 8, which is exactly the geometric mean of 4 and 16. Now, if we take the area of our 4 x 16 rectangle instead, it is the product of 4 and 16 and equals 64. The arithmetic mean of 4 and 16 is 10, and a square with a side of 10 will have the same perimeter as one with sides 4 and 16.

If we have a rectangle with sides 4 and 16, the perimeter of the rectangle is the sum of all four sides: 4 + 4 + 16 + 16 = 40. This formula is used in our calculator.Ī geometric approach to explain the formula is through rectangles and squares. An alternative way to write the formula is (X 1 x X 2. The formula for calculating the geometric mean is: where n is the number of numbers in the set and X 1.X n are the numbers from the first to the n-th. If you are dealing with such tasks, a geometric mean calculator like ours should be most helpful. Consumer Price Index (index of inflation), and others. It is useful in a number of situations where a growth rate is of interest, for example in calculating compound interest rates, financial returns or risk and loses, area and volume averages, in computing indexes such as the U.S. Any time you have several factors contributing to a product, and you want to calculate the "average" of the factors, the answer is the geometric mean. If in an arithmetic mean we combine the numbers using the summation operation and then divide by their number, in a geometric mean we calculate the product of the numbers and then take its n-th root. The geometric mean, often referred to as the geometric average, is a so-called specialized average and is defined as the n-th root of the product of n numbers of the same sign.

Geometric means with zeros in the dataset.


 0 kommentar(er)
0 kommentar(er)
